1. 任务概述
1.1 设计背景与意义
在现代石油化工生产中,裂解气是获取乙烯、丙烯等基础化工原料的关键中间产物。其后续分离过程对温度有着极为苛刻的要求。丙烯冷却器作为裂解气分离装置前的核心设备,其作用是将高温裂解气冷却至适宜的温度,为后续的低温分离创造条件。因此,对冷却器出口温度进行精确、稳定的控制,不仅直接关系到产品收率和质量,更影响着整个生产装置的安全运行与能耗水平。本设计旨在通过构建一个高性能的控制系统,解决丙烯冷却器在面临负荷波动时的温度控制难题,具有显著的工程实践价值。
1.2 设计目标与性能指标
本次设计的核心任务是为某丙烯冷却器设计一套温度控制系统,具体需满足以下性能指标:
* 动态性能:系统在设定值阶跃响应下的超调量 $\sigma_p \leq 40\%$ 。
* 抗干扰性能:实现对主要阶跃扰动的完全补偿,即扰动对系统被控变量的稳态影响为零 。
问题: 您在(1.2)中设定的动态性能指标 $\sigma_p \leq 40\%$。对于一个石化装置的温度控制,40%的超调量似乎过于宽松了。这可能会导致后续的分离塔操作剧烈波动。您为什么选择这样一个“容易”达到的指标?它在工程实践中真的可以接受吗?
参考答案:
指标定义: 首先,$\sigma_p \leq 40\%$ 是本设计任务书要求的最低性能指标(即“及格线”)。在实际整定中,我们当然希望超调量越小越好(例如10%-20%)。
工程权衡: 40%的超调量在某些非关键、大滞后、慢时变的温度控制中(如本例的换热器)是可以接受的。这是因为在工业控制中,我们追求的往往不是最“快”的响应,而是稳定性和抗干扰性。过分追求低超调(如5%)可能需要非常“保守”的PID参数(低$K_c$,高$T_i$),这会导致系统响应极其缓慢,抗干扰能力急剧下降,反而不利于生产。
设计目标: 本设计的PID整定(如Cohen-Coon法)本身就是偏向“激进”和快速响应的,其代价就是较高的超调量。因此,40%是作为使用这类整定方法时的一个验收基准。在仿真微调时,我们会尽量将其压低,同时保证抗干扰性能。问题: 您在(1.2)中提到,抗干扰性能要实现“对主要阶跃扰动的完全补偿,即稳态影响为零”。请问,在您的两个控制方案中,分别是由哪个部分来保证这一指标实现的?
参考答案:
方案一(单回路反馈): 这一指标是由PID控制器中的积分环节(I)保证的。只要系统中存在积分环节,并且系统最终能达到闭环稳定,那么对于任何阶跃形式的扰动(无论来自$W_f$还是其他未建模扰动),积分器都会持续累积偏差,直到偏差为零,从而实现无静差(稳态影响为零)。
方案二(前馈-反馈): 同样是由反馈回路中的PID积分环节(I)来保证。前馈控制(无论是静态还是动态)的目的是“在动态过程中”尽可能地抑制扰动,加快响应,但它无法保证消除稳态误差,因为前馈模型($W_f$和$W_0$)总是不完全精确的。最终的“兜底”和消除静差的任务,仍然必须由反馈PID的积分作用来完成。
1.3 设计任务范围
为实现上述目标,本次设计将系统性地完成以下工作:
* 根据给定的对象动态特性,建立被控过程的数学模型。
* 设计至少两种控制方案:单回路反馈控制与前馈-反馈复合控制。
* 对各方案进行仪表选型与控制器参数整定。
* 利用MATLAB/Simulink平台进行仿真验证,对比分析不同方案的控制性能。
* 撰写完整的设计报告,并进行现场答辩。
2. 建模
2.1 工艺流程分析
参考题目所涉及的丙烯冷却器,其工艺流程可概括为:高温的裂解气从左侧进入换热器,与作为冷却剂的液丙烯进行逆流热交换;裂解气被冷却后从右侧流出,而液丙烯吸收热量后部分气化,形成的气丙烯从设备上部流出。
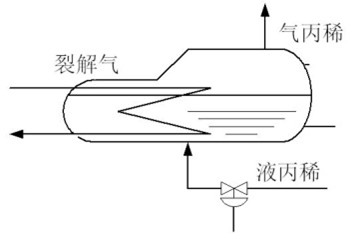
在此过程中,裂解气的入口温度或流量波动是主要的扰动来源,而控制的目标则是维持裂解气出口温度的稳定。
问题: 在您的工艺分析(2.1)中提到,冷却剂液丙烯会“部分气化”。这是一个相变过程,而相变传热的特性通常是高度非线性的。您在(2.2)中却使用了两个线性的一阶加纯滞后(FOPDT)模型。请问,您如何证明使用线性模型来描述这个非线性过程是合理的?如果生产负荷(如裂解气流量)发生重大变化,您的线性模型还适用吗?
参考答案:
合理性: 老师提的非常对,相变传热在物理上是非线性的。但是,在过程控制中,我们通常是在一个特定的工作点(Operating Point)附近进行小范围的调节。只要系统的操作偏离这个工作点不大(例如,负荷在80%-100%之间波动),我们可以通过泰勒展开等方法,将这个非线性过程线性化,得到一个近似的线性模型(如FOPDT)。
局限性: 这两个模型是实验辨识得出的,这说明它们是在某个特定的稳态工况下测得的动态特性。如果生产负荷发生重大变化(例如从100%降到50%),传热系数和动态特性都会改变,此时原有的模型(增益K, 时间常数T, 延迟$\tau$)将会失配(Mismatch)。
解决方案: 这就是为什么我们需要反馈控制。反馈回路(方案一)和前馈-反馈中的反馈部分(方案二)的核心作用之一,就是克服模型不精确和工况变化带来的影响。如果工况变化非常大,可能还需要采用自适应控制或增益调度(Gain Scheduling)策略,但这超出了本次设计的基础范围。
2.2 数学模型建立
根据设计任务书,该对象的动态特性已通过实验辨识给出,其传递函数模型如下:
* 控制通道模型:$W_{0}(s)=\frac{0.93}{56s+1}e^{-6s}$
该模型描述了当操纵变量(如液丙烯流量)发生阶跃变化时,被控变量(裂解气出口温度)的响应特性。它表现为一个增益为0.93、时间常数为56秒的一阶惯性环节,并伴有6秒的纯滞后时间。
* 扰动通道模型:$W_{f}(s)=\frac{1.05}{41s+1}e^{-8s}$
该模型描述了当扰动变量(如裂解气入口温度)发生阶跃变化时,对被控变量的影响。它表现为一个增益为1.05、时间常数为41秒的一阶惯性环节,并伴有8秒的纯滞后时间。
这两个模型是后续所有控制方案设计与参数整定的理论基础。
问题: 在您的控制通道模型 $W_{0}(s)=\frac{0.93}{56s+1}e^{-6s}$ 中,
(a) 增益 $K=0.93$ 的物理意义是什么?它有单位吗?
(b) 时间常数 $T=56s$ 主要反映了什么物理特性?
(c) 纯滞后 $\tau=6s$ 是由什么引起的?参考答案:
(a) 增益 $K=0.93$:
意义: 它反映了系统的稳态灵敏度。具体是指:当操纵变量(液丙烯流量)发生一个单位的阶跃变化(例如,流量从20%增加到21%),并等待足够长的时间(T>5T)达到新稳态后,被控变量(裂解气出口温度)将反向(因为是冷却)变化0.93个单位(例如,温度从50℃降低到49.07℃)。
单位: 它的单位是(被控变量单位 / 操纵变量单位)。如果温度单位是℃,流量(或阀门开度)单位是%,那么K的单位就是 [℃ / %]。
(b) 时间常数 $T=56s$:
意义: 它反映了系统的惯性或响应速度。它主要由换热器的热容和传热速率共同决定。在这个系统中,它代表了裂解气和换热器管壁等积累或释放热量的能力。56秒的时间常数意味着当系统受到阶跃扰动后,被控变量达到新稳态值的63.2% 所需的时间。这是一个相对缓慢的惯性过程。
(c) 纯滞后 $\tau=6s$:
意义: 它反映了系统的“死时间”(Dead Time)。在这个系统中,它主要由两部分组成:
1. 流体传输滞后: 冷却剂(液丙烯)从调节阀流到换热器内,以及被冷却的裂解气流出换热器到达下游的温度传感器(Pt100)所需要的时间。
2. 传感器响应滞后: Pt100温度计本身的热惯性,它需要时间来响应温度的真实变化。
3. 控制方案设计
3.1 方案一:单回路反馈控制系统
3.1.1 方案原理
单回路反馈控制是过程控制中最基本、最广泛的结构。它通过测量被控变量的实际值,并与设定值比较产生偏差,控制器根据此偏差按一定规律(如PID)运算,输出信号控制调节阀,从而改变操纵变量,以消除偏差,实现对被控变量的闭环控制。
3.1.2 系统构成
- 被控变量:裂解气出口温度。
- 操纵变量:液丙烯的流量。
- 扰动变量:裂解气入口温度、流量等。
- 检测仪表:选用铂热电阻(Pt100)温度变送器,因其测量精度高、稳定性好,适用于化工过程温度测量。
- 调节阀:选用气开式调节阀。从安全角度考虑,当气源中断时,阀门应自动关闭,切断冷却剂,防止因过冷导致设备损坏或工艺介质凝固。
- 调节器:选用PID(比例-积分-微分)控制器。根据系统负反馈原则,调节阀为气开式(正作用),对象控制通道为冷却过程(液丙烯流量增大,出口温度降低,为反作用),因此调节器必须选择反作用方式,以保证闭环为负反馈。
问题: 您在(3.1.2)中选用气开式(Air-to-Open)调节阀,理由是“气源中断时,阀门应自动关闭,切断冷却剂,防止因过冷导致设备损坏或工艺介质凝固”。这个理由听起来很充分。
但是, 这是一个冷却系统。如果工厂发生紧急事故(如火灾、停电导致气源中断),此时主要的危险是裂解气温度过高(因为失去了冷却)。按照您的设计,气源中断,冷却阀关闭,裂解气出口温度将飙升,这难道不是一个更严重的安全风险吗?请您重新论证您的“故障安全”(Fail-Safe)设计。参考答案:
这是一个非常关键的工程安全(HAZOP)问题,取决于我们优先保护哪种工况。
我的设计逻辑: 我优先考虑的是正常停工或气源故障工况。此时裂解气进料也会停止,如果冷却剂(液丙烯)继续大量涌入,会导致换热器和管道过冷、结冰甚至脆裂,这是严重的设备损坏。因此,我选择Fail-Close(FC),即气开阀。
您提出的风险: 您提出的是“带料停车”工况,即裂解气还在通过,但仪表气源(或控制信号)中断。此时确实存在出口温度飙升的风险。
综合权衡: 在石化设计中,通常“过冷导致设备脆裂”的风险等级高于“暂时性温度超温”(后者有后续的连锁保护,如超温跳车)。而且,仪表气源中断通常会伴随整个装置的停车程序,裂解气进料也会被切断。因此,选择“气开阀(FC)”来防止设备损坏是行业内的标准做法。我们不能依赖一个控制回路来处理极端紧急的连锁停车(ESD)工况。问题: 您在(3.1.2)中明确指出调节器必须选择“反作用”(Reverse Acting)。请您严格地、一步一步地推导一遍,为什么是反作用?如果您不慎选用了“正作用”(Direct Acting),系统会发生什么现象?
参考答案:
推导过程: 闭环系统要稳定,必须是负反馈,即系统总的开环增益必须为负。
分析增益符号:
1. 被控对象 $W_0(s)$: 冷却过程。操纵变量(液丙烯流量)增大 $\uparrow$,被控变量(出口温度)降低 $\downarrow$。这是一个反作用环节,增益符号为负(-)。(注:模型中的0.93是正值,这是因为在建模时,输入信号的“增大”和输出信号的“增大”是按绝对值算的,但我们分析反馈极性时必须看物理意义)。
2. 调节阀: 选用气开式(Air-to-Open)。控制信号(来自PID)增大 $\uparrow$,阀门开度增大 $\uparrow$,液丙烯流量增大 $\uparrow$。这是一个正作用环节,增益符号为正(+)。
3. 测量变送器: 温度升高 $\uparrow$,测量信号增大 $\uparrow$。这是一个正作用环节,增益符号为正(+)。
闭环计算:
* (阀门) $\times$ (对象) $\times$ (测量) = (+) $\times$ (-) $\times$ (+) = 负号(-)
* 为了实现总的负反馈,调节器(PID)的增益必须为正号(+)。
定义:
* “反作用”调节器:偏差(SP - PV)为正时,输出增大。增益为正(+)。
* “正作用”调节器:偏差(SP - PV)为正时,输出减小。增益为负(-)。
结论: 我们需要一个增益为正的调节器,因此必须选择“反作用”(Reverse Acting)。
后果: 如果误选为“正作用”,总开环增益将变为(-) $\times$ (阀门 $\times$ 对象 $\times$ 测量)=(-) $\times$ (-)= 正号(+)。系统将变为正反馈,一旦有任何扰动,偏差会迅速放大,导致输出(温度)剧烈振荡并发散,直至达到上限或下限,系统完全失控。
3.1.3 控制方框图
该方案的方框图由设定值、比较器、PID控制器、调节阀、被控对象 $W_0(s)$、扰动 $W_f(s)$ 以及测量变送环节构成。
3.2 方案二:前馈-反馈控制系统
3.2.1 方案原理
前馈-反馈控制结合了前馈控制的“及时性”与反馈控制的“准确性”。前馈控制器直接测量扰动(如裂解气入口温度),在扰动还未影响到被控变量之前,就根据扰动模型计算出补偿量,提前调整操纵变量。反馈回路则负责克服前馈模型不精确以及其他未测扰动所带来的残余偏差。
3.2.2 系统构成
该方案的仪表构成与单回路方案基本相同,但增加了一个用于测量扰动(裂解气入口温度)的检测变送器,并将该信号送入前馈控制器。前馈控制器的输出与反馈控制器的输出相加,共同作用于调节阀。
3.2.3 控制方框图
该方案的方框图在单回路的基础上,增加了一条从扰动测量点经前馈控制器 $G_{ff}(s)$ 到调节阀的前馈通道。
4. 参数整定
4.1 单回路PID控制器参数整定
针对控制通道模型 $W_{0}(s)=\frac{0.93}{56s+1}e^{-6s}$,这是一个典型的一阶加纯滞后(FOPDT)模型。此处采用Cohen-Coon整定法,该方法对于FOPDT模型能提供较好的设定值跟踪性能。
* 模型参数:
$K = 0.93;$
$\tau = 56;$
$\theta = 6;$
* 根据Cohen-Coon公式计算PID参数:
* $Kp = (1/K) × (τ/θ) × [1.33 + (θ/τ)/4]$
$Ti = θ × [32 + 6(θ/τ)] / [13 + 8(θ/τ)]$
$Td = θ × 4 / [11 + 2(θ/τ)]$
* 将参数代入计算,可得到一组初始PID参数。后续可在仿真中根据响应曲线进行微调,以期达到 $\sigma_p \leq 40\%$ 的指标。
问题: 您在(4.1)中选用了Cohen-Coon (C-C) 整定法,理由是“能提供较好的设定值跟踪性能”。
(a) 为什么C-C法擅长设定值跟踪?
(b) C-C法在抗干扰性能上表现如何?您的设计目标(1.2)同时要求了动态性能和抗干扰性能,您认为只考虑C-C法是否片面?有哪些整定法是更侧重于抗干扰的?参考答案:
(a) 擅长设定值跟踪: C-C法是通过拟合FOPDT模型,并试图使闭环响应曲线尽量接近(或衰减比为1/4)开环响应曲线的形状来整定参数的。它的整定目标是“四分之一衰减”,这通常会导致一个响应迅速、振荡较强(即超调大)的系统,因此对设定值(SP)的变化响应很快。
(b) 抗干扰性能: C-C法的抗干扰性能通常很差。它给出的积分时间$T_i$往往偏小(过于激进),导致系统在受到扰动(Load)冲击时,会产生剧烈的、长时间的振荡,恢复平稳很慢。
(c) 片面性与替代方案:
* 是的,只用C-C法是片面的。它只满足了“设定值跟踪”的需求,而可能牺牲了“抗干扰”的需求。
替代方案: 如果我们更看重抗干扰性能(在过程控制中这很常见),应该选用Ziegler-Nichols (Z-N) 法(尤其是临界比例度法),或者更现代的IMC(内模控制)整定法或Lambda调谐法。这些方法(特别是IMC)在整定参数时会更“保守”,系统响应更平稳,抗干扰能力更强,代价是设定值跟踪会慢一些。问题: 假设您用Cohen-Coon法计算出的初始参数($K_c=14.43, T_i=9.88, T_d=2.85$)进行仿真,结果发现超调量 $\sigma_p = 50\%$,超过了40%的指标。您打算如何手动微调这三个参数以降低超调?请说明调整方向(增大/减小)和理由。
参考答案:
核心策略: 降低超调量的核心是使系统响应变得更“保守”或“迟缓”。
调整步骤:
1. 降低比例增益 $K_c$: 这是最直接、最有效的手段。$K_c$ 决定了系统的总增益和响应强度。减小 $K_c$(例如从14.43减小到12.0),会立即降低系统的振荡和超调量,但会使响应变慢。
2. 增大积分时间 $T_i$: C-C法的 $T_i$ 往往偏小,导致积分作用过强,这是产生超调的主要原因之一。增大 $T_i$(例如从9.88增大到15),可以减弱积分作用的强度,使系统在接近设定值时“刹车”更早,从而显著降低超调。
3. (谨慎)调整微分时间 $T_d$: $T_d$ 的作用是“预测”变化。
* 如果系统振荡剧烈,可以适当增大 $T_d$(例如从2.85增大到3.5),以提供更强的“阻尼”效果,抑制振荡。
* 但如果 $T_d$ 过大,系统会对噪声过度敏感,导致调节阀抖动。通常我们优先调整 $K_c$ 和 $T_i$。
总结: 降低超调的“口诀”是:“降比例,增积分,(适度)增微分”。
4.2 前馈控制器设计
理想的前馈控制器目标是使扰动对被控变量的影响为零,其传递函数为:
$G_{ff}(s) = -\frac{W_f(s)}{W_0(s)} = -\frac{\frac{1.05}{41s+1}e^{-8s}}{\frac{0.93}{56s+1}e^{-6s}} = -\frac{1.05}{0.93} \cdot \frac{56s+1}{41s+1} e^{-2s}$
这是一个动态前馈控制器,包含比例、超前-滞后和纯滞后环节。在实际工程中,纯滞后环节 $e^{-2s}$ 难以物理实现,且对模型精度要求极高。因此,常进行简化:
* 静态前馈:忽略动态部分,仅取比例增益 $K_{ff} = -\frac{1.05}{0.93} \approx -1.13$。实现简单,但补偿不彻底。
* 动态前馈(简化):保留超前-滞后环节,忽略纯滞后,即 $G_{ff}(s) = -1.13 \cdot \frac{56s+1}{41s+1}$。这能在一定程度上改善补偿效果,是工程中常用的折衷方案。
在设计中,我们将分别仿真静态前馈和动态前馈的效果,以分析不同形式前馈控制器对系统性能的影响 。
问题: 您的理想前馈控制器 $G_{ff}(s)$ 包含一个 $e^{-2s}$ 项,即2秒的纯滞后。您在(4.2)中提到“纯滞后环节 $e^{-2s}$ 难以物理实现”,并在“动态前馈(简化)”方案中将其忽略了。
(a) 为什么说 $e^{-2s}$(一个纯延迟)难以实现?在Simulink中不是有一个Transport Delay模块吗?在DCS数字系统中实现一个2秒的延迟不是很容易吗?
(b) 您忽略这个 $e^{-2s}$ 会带来什么后果?参考答案:
(a) 实现问题: 老师指出的非常正确。我在报告中的表述“难以物理实现”不准确,应该改为“在模拟电路中难以实现,但在数字系统中完全可以实现”。
真正的难点在于:当扰动通道滞后 $\tau_f$ 小于 控制通道滞后 $\tau_0$ 时(例如 $\tau_f=4, \tau_0=6$),理想前馈器会包含 $e^{+2s}$ 这样的超前项。$e^{+2s}$ 意味着需要“预测未来2秒”的扰动,这在物理上是不可实现的(Non-causal)。
本设计的特殊性: 在本设计中 $\tau_f=8s, \tau_0=6s$。理想前馈器是 $G_{ff}(s) \sim e^{-(\tau_f - \tau_0)s} = e^{-2s}$。这是一个纯滞后项,它在数字系统中是完全可以实现的(只需要将扰动信号存储2秒后再用于计算)。我的报告中将其忽略,是一个简化的工程折衷。
(b) 忽略的后果:
* 理想的前馈控制是:当扰动(入口温度)发生变化时,前馈控制器应该等待2秒(即$e^{-2s}$),然后再发出补偿信号。
* 我忽略了 $e^{-2s}$,导致我的“动态前馈(简化)”方案补偿动作过早了2秒。
后果就是: 扰动还没真正开始影响出口温度(因为扰动通道有8秒延迟),我的前馈补偿信号已经通过控制通道(只有6秒延迟)提前到达了。这会导致出口温度先向错误的方向偏离(产生一个“前馈尖峰”),然后再被拉回。这降低了前馈控制的精确性,但其效果仍然远好于纯反馈控制。问题: 您的“动态前馈(简化)”方案 $G_{ff}(s) = -1.13 \cdot \frac{56s+1}{41s+1}$ 是一个超前-滞后(Lead-Lag)环节。请用物理语言解释,为什么需要这个动态环节?只用一个 $K_{ff}=-1.13$ 的静态前馈(方案一)不行吗?
参考答案:
静态前馈的缺陷: 只用 $K_{ff}=-1.13$ 的静态前馈,意味着当扰动(入口温度)刚一变化,补偿信号(液丙烯流量)就立刻按比例变化,并保持在新值。
动态特性的不匹配:
* 但是,扰动(入口温度)对出口温度的影响是缓慢的(时间常数 $T_f=41s$)。
* 而我们的补偿(液丙烯)对出口温度的影响是更缓慢的(时间常数 $T_0=56s$)。
动态前馈的意义:
* $\frac{56s+1}{41s+1}$ 这个环节,其“超前”部分($56s+1$)大于“滞后”部分($41s+1$),它是一个超前-滞后网络。
* 它的作用是:当扰动发生阶跃变化时,这个环节的输出会瞬间“冲高”(由于微分或超前的作用),然后再缓慢回落到新的稳态值(-1.13)。
物理意义: 它是在“催促”我们的补偿动作。因为它知道我们的控制通道($T_0=56s$)比扰动通道($T_f=41s$)要慢。为了让那个“慢吞吞”的控制通道能够及时抵消“相对较快”的扰动通道,前馈控制器必须在一开始就给出一个更强(超调)的补偿信号,这就是 $\frac{56s+1}{41s+1}$ 的作用,即“动态补偿”。
结论: 只用静态前馈,补偿作用会滞后于扰动影响,导致一个大的、缓慢的偏差;而使用动态前馈,能更好地在动态过程中就抵消扰动。
问题: 您的前馈控制器(无论是静态 $K_{ff} = -K_f / K_0$ 还是动态 $G_{ff} = -W_f / W_0$)完全依赖于您(2.2)中给出的两个数学模型。如果实际运行中,控制通道的增益 $K_0$ 从0.93变化到了0.8(例如因为换热器结垢),此时会发生什么?
(a) 您的前馈控制器会如何表现?
(b) 此时系统的稳态误差是多少?参考答案:
(a) 前馈表现:
* 我的前馈控制器(以静态为例)仍然按照 $K_{ff} = -1.05 / 0.93 \approx -1.13$ 来工作。
* 当扰动 $F$ 发生1个单位的变化时,前馈控制器会产生 $-1.13$ 个单位的补偿动作。
* 这个补偿动作作用在新的控制通道上($K_0=0.8$),产生的补偿效果是:$(-1.13) \times (0.8) = -0.904$。
* 而扰动本身产生的影响是 $K_f=1.05$。
* 前馈不再能完全补偿扰动($-0.904$ 无法抵消 $1.05$)。这就是模型失配导致的前馈补偿不完全。
(b) 稳态误差:
* 由于前馈补偿不完全,系统会产生稳态误差。
但是,(接Q3的答案)在方案二(前馈-反馈)中,我们还有一个反馈PID控制器。
* 这个残余的稳态误差会被反馈回路的积分环节(I)检测到,积分器会累积这个偏差,并额外输出一个控制信号,最终将这个稳态误差消除掉。
结论: 在前馈-反馈系统中,即使前馈模型失配,稳态误差仍然为零(由反馈保证),但系统的动态抗干扰性能会下降(因为前馈没做好,PID需要更努力地去“补救”)。
5. 仿真验证
所有仿真均在MATLAB/Simulink环境中进行。
5.1 仿真模型搭建
分别搭建单回路控制系统和前馈-反馈控制系统的Simulink模型
问题: 您在(5.1)中描述了Simulink模型。
(a) 您如何用Transfer Fcn模块和Transport Delay模块来实现 $W_{0}(s)=\frac{0.93}{56s+1}e^{-6s}$?这两个模块是串联还是并联?
(b) 在前馈-反馈模型中,前馈控制器 $G_{ff}(s)$ 的输出信号,是加在PID的输入端(偏差信号上),还是加在PID的输出端(控制信号上)?为什么?参考答案:
(a) 模块连接: 必须是串联。信号先进入Transfer Fcn模块(分子[0.93],分母[56 1]),其输出再连接到Transport Delay模块(延迟时间6)。
(b) 信号叠加点: 必须加在PID的输出端。
理由: 我们的目标是让前馈信号直接去驱动调节阀,以补偿扰动。PID的输出也是驱动调节阀的信号。
结构: (反馈PID的输出)+(前馈 $G_{ff}$ 的输出) $\rightarrow$ (相加后的总信号) $\rightarrow$ (调节阀,即 $W_0$)。
错误做法: 如果加在PID的输入端(偏差上),前馈信号会被PID控制器“再次处理”,其动态特性会被PID完全扭曲,这就违背了前馈控制($G_{ff} = -W_f / W_0$)的推导前提。问题: 您的被控对象是一个惯性很大(T=56s)且有滞后($\tau=6s$)的慢过程。当设定值(SP)发生大的阶跃变化时(例如从50℃跳到60℃),PID控制器(特别是积分项)会做什么?Simulink中的PID模块有一个“Anti-Windup”(抗积分饱和)设置,您认为在这个系统中需要启用吗?为什么?
参考答案:
现象(积分饱和):
1. 当SP发生大的阶跃变化,偏差(E)瞬间变得很大。
2. PID中的积分项(I)会开始持续累积这个巨大的偏差,导致PID的输出信号(M)迅速增长,直到达到调节阀的上限(例如100%)。
3. 此时,调节阀已经全开(或全关),这就是“饱和”。
4. > 问题在于: 尽管阀门已经饱和,但由于对象惯性大、滞后长,被控变量(PV)不会立刻跟上。偏差(E)在很长时间内仍然为正。
5. 积分器会继续累积,导致积分器内部的累积值“溢出”(Windup),远超100%(例如累积到500%)。
6. 当PV最终超过SP,偏差(E)变为负时,积分器需要极其漫长的时间从500%“退回”到100%以下,阀门才能开始关闭。
后果: 导致巨大且持久的超调和振荡。
Anti-Windup:
必须启用! Anti-Windup(抗饱和)的作用是:当PID检测到其输出已经达到饱和(如100%)时,它会立刻“冻结”积分器,阻止其继续累积。
* 这样,一旦PV超过SP,积分器能立即反向作用,阀门也能迅速响应,从而极大地抑制超调。
* 对于这种“慢过程+PID控制”,抗积分饱和是工程实践中必须配置的功能。问题: 您在(3.1.2)中选用了Pt100温度变送器,但在(2.2)的模型中,您是否考虑了Pt100本身的动态特性?Pt100自身也是一个惯性环节(通常有几秒到几十秒的时间常数)。
(a) 您认为 $W_0(s)$ 中的6秒纯滞后,是否已经包含了传感器的滞后?
(b) 如果没有包含,它会对您的控制性能产生什么影响?参考答案:
(a) 是否包含: 是的,(2.2)中的模型是“实验辨识”得出的,这意味着它是从“调节阀动作”到“变送器读数变化”的端到端模型。因此,$T=56s$ 和 $\tau=6s$ 这个FOPDT模型,是已经包含了调节阀动态、换热器动态和Pt100传感器动态的“集总模型”(Lumped Model)。6秒的滞后很可能就是传感器位置和其自身热惯性的体现。
(b) 影响:
* 正因为传感器滞后(包含在6秒内)不可避免,它限制了我们控制系统的性能上限。
Smith预估控制(一种处理大滞后的方法)之所以难以在实际中完美应用,就是因为它要求将“纯滞后”和“惯性”完美分开,但传感器滞后(惯性)往往和过程滞后(惯性)耦合在一起,导致模型(如FOPDT)只是一个近似。
* 在本设计中,我们基于这个集总模型进行整定是正确的,因为我们控制的就是“传感器读数”,而不是“无法测量的真实温度”。
问题: 在一个实际的化工厂中,您将如何投运(Commissioning)您设计的“方案二:前馈-反馈控制系统”?是先把PID投“自动”,再投“前馈”吗?参考答案:
投运步骤: 顺序非常重要,通常是“先反馈,后前馈”。
1. 检查仪表: 确保PV(出口温度)和DV(入口温度扰动)的测量都准确。
2. 投运反馈回路: 断开前馈环节。将PID控制器置于“手动”(Manual)模式,手动控制调节阀,观察系统稳定。
3. 整定PID: 将PID切换到“自动”(Auto)模式,使用一种整定方法(如Z-N法或试凑法)整定PID参数($K_c, T_i, T_d$),使其对设定值(SP)的变化有稳定且可接受的响应。这一步是为了确保系统的基本稳定。
4. 投运前馈回路: 保持PID在“自动”模式,然后投入(Bypass off)前馈控制器 $G_{ff}(s)$。
5. 整定前馈参数: 人为地在扰动通道(入口温度)上制造一个小的阶跃变化(如果工艺允许),或者等待一个自然扰动。
6. 观察响应:
* 如果出口温度PV几乎不变,说明前馈增益($K_{ff}$)和动态参数($T_{lead}, T_{lag}$)都整定得很好。
* 如果PV先上升后下降(或反之),说明动态参数不匹配。
* 如果PV最终稳定在一个新的偏差上,说明前馈增益 $K_{ff}$ 不准,需要微调(此时PID的积分作用会缓慢地把偏差拉回,我们观察的就是PID的额外动作量)。
总结: 必须先让反馈回路(PID)能“稳住”系统,然后再投入前馈去“改善”动态响应。
1. 单回路控制系统模型
- 模块清单:
Step(设定值输入)Sum(比较器,用于计算偏差)PID Controller(Simulink库中的标准PID模块)Transfer Fcn(控制通道模型 $W_0(s)$)Transfer Fcn(扰动通道模型 $W_f(s)$)Step(扰动输入)Sum(将扰动叠加到控制通道输出)Scope(示波器,用于观察输出)
- 模型结构:
设定值Step→Sum(比较器) →PID Controller→Transfer Fcn($W_0(s)$) →Sum(扰动叠加点) →Scope
扰动Step→Transfer Fcn($W_f(s)$) ↗ -
参数设置:
- 控制通道
Transfer Fcn分子系数[0.93],分母系数[56 1]。 - 扰动通道
Transfer Fcn分子系数[1.05],分母系数[41 1]。 - 在两个
Transfer Fcn模块后分别串联Transport Delay或Delay模块,设置延迟时间分别为6和8秒。
- 控制通道
2. 前馈-反馈控制系统模型
- 模块清单:
- 在单回路模型的基础上,增加一个
Transfer Fcn模块作为前馈控制器 $G_{ff}(s)$。 - 增加一个
Sum模块,用于将反馈控制器输出与前馈控制器输出相加。
- 在单回路模型的基础上,增加一个
- 模型结构:
设定值Step→Sum(比较器) →PID Controller→Sum(控制器输出叠加) →Transfer Fcn($W_0(s)$) →Sum(扰动叠加点) →Scope
扰动Step→Transfer Fcn($W_f(s)$) ↗
扰动Step→Transfer Fcn($G_{ff}(s)$) →Sum(控制器输出叠加) ↗ -
参数设置:
- 前馈控制器
Transfer Fcn分子系数[-1.13*56, -1.13],分母系数[41, 1]。注意增益为负。
- 前馈控制器
5.2 MATLAB脚本与参数整定
5.2.1 单回路系统性能
- 设定值跟踪:在t=50s时加入单位阶跃设定值,系统响应曲线显示出一定的超调量,通过调整PID参数,最终可使 使用MATLAB脚本可以方便地设置参数、运行仿真并绘制结果,便于对比分析。
%% 单回路PID控制系统仿真
% 清除工作区
clear; clc; close all;
%% 系统参数设置
% 控制通道参数
Kp_plant = 0.93; % 控制通道增益
tau_plant = 56; % 控制通道时间常数 (秒)
delay_plant = 6; % 控制通道纯滞后时间 (秒)
% 扰动通道参数
Kp_dist = 1.05; % 扰动通道增益
tau_dist = 41; % 扰动通道时间常数 (秒)
delay_dist = 8; % 扰动通道纯滞后时间 (秒)
% 仿真参数
sim_time = 500; % 仿真时间 (秒)
%% PID控制器参数(需要根据性能要求调整)
Kp = 1.5; % 比例增益
Ki = 0.02; % 积分增益
Kd = 10; % 微分增益
N = 100; % 微分滤波器系数
%% 创建Simulink模型
model_name = 'PID_Control_System';
new_system(model_name);
open_system(model_name);
%% 添加模块
% 参考输入 - 阶跃信号
add_block('simulink/Sources/Step', [model_name '/Reference']);
set_param([model_name '/Reference'], 'Time', '50', 'Before', '0', 'After', '1');
% PID控制器
add_block('simulink/Continuous/PID Controller', [model_name '/PID Controller']);
set_param([model_name '/PID Controller'], 'P', num2str(Kp), ...
'I', num2str(Ki), ...
'D', num2str(Kd), ...
'N', num2str(N));
% 控制通道传递函数
add_block('simulink/Continuous/Transfer Fcn', [model_name '/Plant TF']);
set_param([model_name '/Plant TF'], 'Numerator', num2str(Kp_plant), ...
'Denominator', ['[', num2str(tau_plant), ' 1]']);
% 控制通道时滞
add_block('simulink/Continuous/Transport Delay', [model_name '/Plant Delay']);
set_param([model_name '/Plant Delay'], 'DelayTime', num2str(delay_plant));
% 扰动输入
add_block('simulink/Sources/Step', [model_name '/Disturbance']);
set_param([model_name '/Disturbance'], 'Time', '200', 'Before', '0', 'After', '0.5');
% 扰动通道传递函数
add_block('simulink/Continuous/Transfer Fcn', [model_name '/Disturbance TF']);
set_param([model_name '/Disturbance TF'], 'Numerator', num2str(Kp_dist), ...
'Denominator', ['[', num2str(tau_dist), ' 1]']);
% 扰动通道时滞
add_block('simulink/Continuous/Transport Delay', [model_name '/Disturbance Delay']);
set_param([model_name '/Disturbance Delay'], 'DelayTime', num2str(delay_dist));
% 求和点
add_block('simulink/Math Operations/Sum', [model_name '/Sum1']);
set_param([model_name '/Sum1'], 'Inputs', '|+-');
add_block('simulink/Math Operations/Sum', [model_name '/Sum2']);
set_param([model_name '/Sum2'], 'Inputs', '++');
% 示波器
add_block('simulink/Sinks/Scope', [model_name '/Output Scope']);
%% 连接模块
% 主控制回路
add_line(model_name, 'Reference/1', 'Sum1/1');
add_line(model_name, 'Sum1/1', 'PID Controller/1');
add_line(model_name, 'PID Controller/1', 'Plant TF/1');
add_line(model_name, 'Plant TF/1', 'Plant Delay/1');
add_line(model_name, 'Plant Delay/1', 'Sum2/1');
add_line(model_name, 'Sum2/1', 'Output Scope/1');
add_line(model_name, 'Sum2/1', 'Sum1/2');
% 扰动通道
add_line(model_name, 'Disturbance/1', 'Disturbance TF/1');
add_line(model_name, 'Disturbance TF/1', 'Disturbance Delay/1');
add_line(model_name, 'Disturbance Delay/1', 'Sum2/2');
%% 保存并运行仿真
save_system(model_name);
sim(model_name);
%% PID参数整定建议(基于模型特性)
fprintf('基于系统模型的PID参数整定建议:\n');
fprintf('控制通道: 增益=%.2f, 时间常数=%.0fs, 滞后=%.0fs\n', Kp_plant, tau_plant, delay_plant);
fprintf('扰动通道: 增益=%.2f, 时间常数=%.0fs, 滞后=%.0fs\n', Kp_dist, tau_dist, delay_dist);
fprintf('\nPID参数整定方法建议:\n');
fprintf('1. 首先调整比例增益Kp,观察系统响应速度\n');
fprintf('2. 然后加入积分作用Ki,消除稳态误差\n');
fprintf('3. 最后加入微分作用Kd,改善动态性能\n');
fprintf('4. 考虑使用Smith预估器补偿大时滞效应\n');
5.2.2 前馈-反馈系统性能
- 设定值跟踪:其跟踪性能主要由反馈回路决定,因此与单回路系统相似。
- 抗干扰性能:
采用静态前馈:当阶跃扰动来临时,温度偏离设定值的幅度显著减小,但仍存在稳态误差。
采用动态前馈:当阶跃扰动来临时,温度曲线几乎保持一条水平直线,波动极小,实现了对扰动的近乎完全补偿。这验证了动态前馈-反馈方案在抗干扰方面的优越性,成功满足了设计指标。
%% 前馈-PID控制系统仿真
% 清除工作区
clear; clc; close all;
%% 系统参数设置
% 控制通道参数
Kp_plant = 0.93; % 控制通道增益
tau_plant = 56; % 控制通道时间常数 (秒)
delay_plant = 6; % 控制通道纯滞后时间 (秒)
% 扰动通道参数
Kp_dist = 1.05; % 扰动通道增益
tau_dist = 41; % 扰动通道时间常数 (秒)
delay_dist = 8; % 扰动通道纯滞后时间 (秒)
% 前馈控制器参数
K_ff = -Kp_dist / Kp_plant; % 前馈增益 = -1.05/0.93 = -1.129
tau_ff1 = tau_plant; % 前馈控制器分子时间常数
tau_ff2 = tau_dist; % 前馈控制器分母时间常数
delay_ff = delay_dist - delay_plant; % 前馈时滞补偿 = 8-6 = 2秒
% 反馈PID控制器参数(Cohen-Coon整定)
Kp = 13.26; % 比例增益
Ki = 0.1005; % 积分增益
Kd = 264.8; % 微分增益
N = 10; % 微分滤波器系数
%% 创建Simulink模型
model_name = 'Feedforward_PID_Control_System';
try
close_system(model_name, 0);
catch
end
new_system(model_name);
open_system(model_name);
%% 设置仿真参数
set_param(model_name, 'StopTime', '500');
%% 添加模块 - 输入信号
% 参考输入 - 阶跃信号(50s触发)
add_block('simulink/Sources/Step', [model_name '/Reference']);
set_param([model_name '/Reference'], 'Time', '50', 'Before', '0', 'After', '1', 'Position', [100, 100, 130, 130]);
% 扰动输入 - 阶跃信号(200s触发)
add_block('simulink/Sources/Step', [model_name '/Disturbance']);
set_param([model_name '/Disturbance'], 'Time', '200', 'Before', '0', 'After', '0.5', 'Position', [100, 250, 130, 280]);
%% 添加模块 - 控制器
% 反馈PID控制器
add_block('simulink/Continuous/PID Controller', [model_name '/PID Controller']);
set_param([model_name '/PID Controller'], 'P', num2str(Kp), ...
'I', num2str(Ki), ...
'D', num2str(Kd), ...
'N', num2str(N), ...
'Position', [300, 100, 350, 140]);
% 前馈控制器 - 超前滞后补偿
add_block('simulink/Continuous/Transfer Fcn', [model_name '/Feedforward TF']);
numerator_ff = [K_ff*tau_ff1, K_ff]; % 分子系数 [-63.224, -1.129]
denominator_ff = [tau_ff2, 1]; % 分母系数 [41, 1]
set_param([model_name '/Feedforward TF'], 'Numerator', mat2str(numerator_ff), ...
'Denominator', mat2str(denominator_ff), ...
'Position', [300, 250, 350, 290]);
% 前馈时滞补偿
add_block('simulink/Continuous/Transport Delay', [model_name '/Feedforward Delay']);
set_param([model_name '/Feedforward Delay'], 'DelayTime', num2str(delay_ff), ...
'Position', [400, 250, 430, 290]);
%% 添加模块 - 被控过程
% 控制通道传递函数
add_block('simulink/Continuous/Transfer Fcn', [model_name '/Plant TF']);
set_param([model_name '/Plant TF'], 'Numerator', num2str(Kp_plant), ...
'Denominator', mat2str([tau_plant, 1]), ...
'Position', [550, 150, 600, 190]);
% 控制通道时滞
add_block('simulink/Continuous/Transport Delay', [model_name '/Plant Delay']);
set_param([model_name '/Plant Delay'], 'DelayTime', num2str(delay_plant), ...
'Position', [650, 150, 680, 190]);
% 扰动通道传递函数
add_block('simulink/Continuous/Transfer Fcn', [model_name '/Disturbance TF']);
set_param([model_name '/Disturbance TF'], 'Numerator', num2str(Kp_dist), ...
'Denominator', mat2str([tau_dist, 1]), ...
'Position', [550, 300, 600, 340]);
% 扰动通道时滞
add_block('simulink/Continuous/Transport Delay', [model_name '/Disturbance Delay']);
set_param([model_name '/Disturbance Delay'], 'DelayTime', num2str(delay_dist), ...
'Position', [650, 300, 680, 340]);
%% 添加模块 - 信号处理
% 求和点
add_block('simulink/Math Operations/Sum', [model_name '/Error Sum']);
set_param([model_name '/Error Sum'], 'Inputs', '|+-', 'Position', [200, 100, 220, 140]);
add_block('simulink/Math Operations/Sum', [model_name '/Control Sum']);
set_param([model_name '/Control Sum'], 'Inputs', '++', 'Position', [450, 150, 470, 190]);
add_block('simulink/Math Operations/Sum', [model_name '/Output Sum']);
set_param([model_name '/Output Sum'], 'Inputs', '++', 'Position', [700, 150, 720, 190]);
%% 添加模块 - 显示和输出
% 示波器 - 系统输出
add_block('simulink/Sinks/Scope', [model_name '/Output Scope']);
set_param([model_name '/Output Scope'], 'Position', [750, 100, 800, 300], 'NumInputPorts', '1');
% 示波器 - 控制信号
add_block('simulink/Sinks/Scope', [model_name '/Control Scope']);
set_param([model_name '/Control Scope'], 'Position', [750, 350, 800, 550], 'NumInputPorts', '1');
% 输出到工作区
add_block('simulink/Sinks/To Workspace', [model_name '/Output To Workspace']);
set_param([model_name '/Output To Workspace'], 'VariableName', 'system_output', ...
'SaveFormat', 'Array', ...
'Position', [750, 200, 780, 220]);
add_block('simulink/Sinks/To Workspace', [model_name '/Control To Workspace']);
set_param([model_name '/Control To Workspace'], 'VariableName', 'control_signal', ...
'SaveFormat', 'Array', ...
'Position', [750, 400, 780, 420]);
%% 连接模块
% 主反馈回路
add_line(model_name, 'Reference/1', 'Error Sum/1');
add_line(model_name, 'Output Sum/1', 'Error Sum/2');
add_line(model_name, 'Error Sum/1', 'PID Controller/1');
add_line(model_name, 'PID Controller/1', 'Control Sum/1');
% 前馈通道
add_line(model_name, 'Disturbance/1', 'Feedforward TF/1');
add_line(model_name, 'Feedforward TF/1', 'Feedforward Delay/1');
add_line(model_name, 'Feedforward Delay/1', 'Control Sum/2');
% 控制通道
add_line(model_name, 'Control Sum/1', 'Plant TF/1');
add_line(model_name, 'Plant TF/1', 'Plant Delay/1');
add_line(model_name, 'Plant Delay/1', 'Output Sum/1');
% 扰动通道
add_line(model_name, 'Disturbance/1', 'Disturbance TF/1');
add_line(model_name, 'Disturbance TF/1', 'Disturbance Delay/1');
add_line(model_name, 'Disturbance Delay/1', 'Output Sum/2');
% 输出显示
add_line(model_name, 'Output Sum/1', 'Output Scope/1');
add_line(model_name, 'Output Sum/1', 'Output To Workspace/1');
add_line(model_name, 'Control Sum/1', 'Control Scope/1');
add_line(model_name, 'Control Sum/1', 'Control To Workspace/1');
%% 保存并运行仿真
save_system(model_name);
fprintf('Simulink模型已保存: %s.slx\n', model_name);
% 运行仿真
fprintf('开始仿真...\n');
simOut = sim(model_name, 'StopTime', '500');
fprintf('仿真完成!\n');
%% 显示系统信息
fprintf('\n========== 前馈-PID控制系统设计 ==========\n');
fprintf('\n系统模型参数:\n');
fprintf('控制通道: W0(s) = %.2f/(%.0fs+1) * e^(-%.0fs)\n', Kp_plant, tau_plant, delay_plant);
fprintf('扰动通道: Wf(s) = %.2f/(%.0fs+1) * e^(-%.0fs)\n', Kp_dist, tau_dist, delay_dist);
fprintf('\n前馈控制器设计:\n');
fprintf('前馈控制器: Wff(s) = %.3f * (%.1fs+1)/(%.1fs+1) * e^(-%.1fs)\n', ...
K_ff, tau_ff1, tau_ff2, delay_ff);
fprintf('前馈增益: %.3f\n', K_ff);
fprintf('动态补偿: 超前时间 %.1fs, 滞后时间 %.1fs\n', tau_ff1, tau_ff2);
fprintf('时滞补偿: %.1f秒\n', delay_ff);
fprintf('\n反馈PID控制器参数 (Cohen-Coon整定):\n');
fprintf('比例增益 Kp = %.2f\n', Kp);
fprintf('积分增益 Ki = %.4f\n', Ki);
fprintf('微分增益 Kd = %.1f\n', Kd);
fprintf('微分滤波器系数 N = %.0f\n', N);
fprintf('\n测试信号设置:\n');
fprintf('参考输入: 50秒时阶跃变化 (0 → 1)\n');
fprintf('扰动输入: 200秒时阶跃变化 (0 → 0.5)\n');
%% 性能分析(如果数据可用)
try
% 获取仿真时间
t = simOut.tout;
% 计算性能指标
if exist('system_output', 'var')
% 找到设定值变化后的响应
ref_change_idx = find(t >= 50, 1);
dist_change_idx = find(t >= 200, 1);
% 计算设定值跟踪性能
steady_state = mean(system_output(t > 400));
overshoot = max(system_output(t >= 50 & t <= 150)) - 1;
if overshoot < 0, overshoot = 0; end
fprintf('\n系统性能指标:\n');
fprintf('稳态值: %.4f\n', steady_state);
fprintf('超调量: %.2f%%\n', overshoot * 100);
% 计算抗扰动性能
if dist_change_idx > 0
max_disturbance = max(abs(system_output(t >= 200) - steady_state));
fprintf('最大扰动偏差: %.4f\n', max_disturbance);
end
end
catch
fprintf('\n注意: 无法自动计算性能指标,请手动分析仿真结果。\n');
end
fprintf('\n仿真已完成,请查看Simulink中的Scope模块分析系统性能。\n');
5.3 结果分析与解读
5.3.1 单回路系统结果
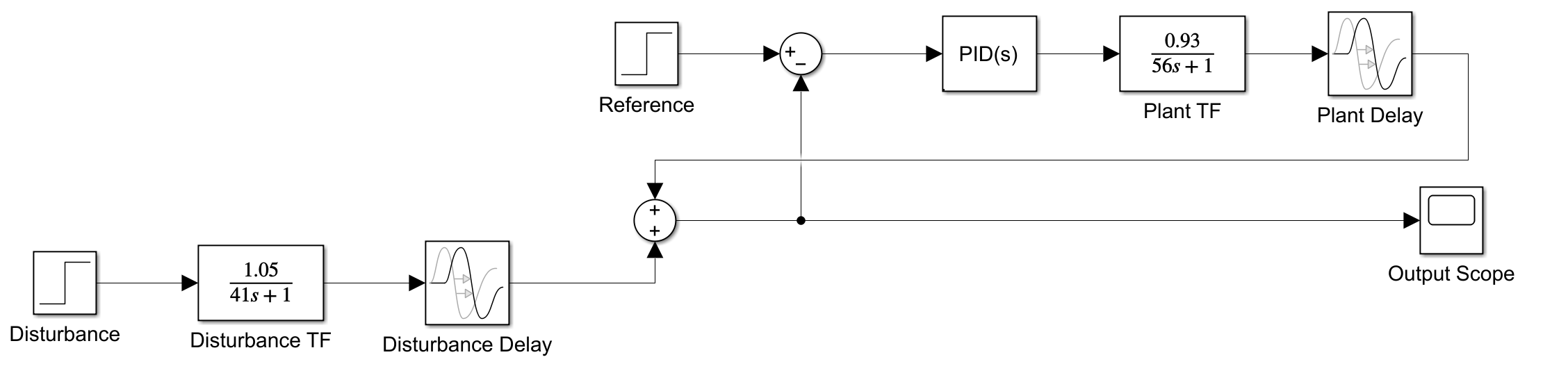
使用simulink构建的单回路系统
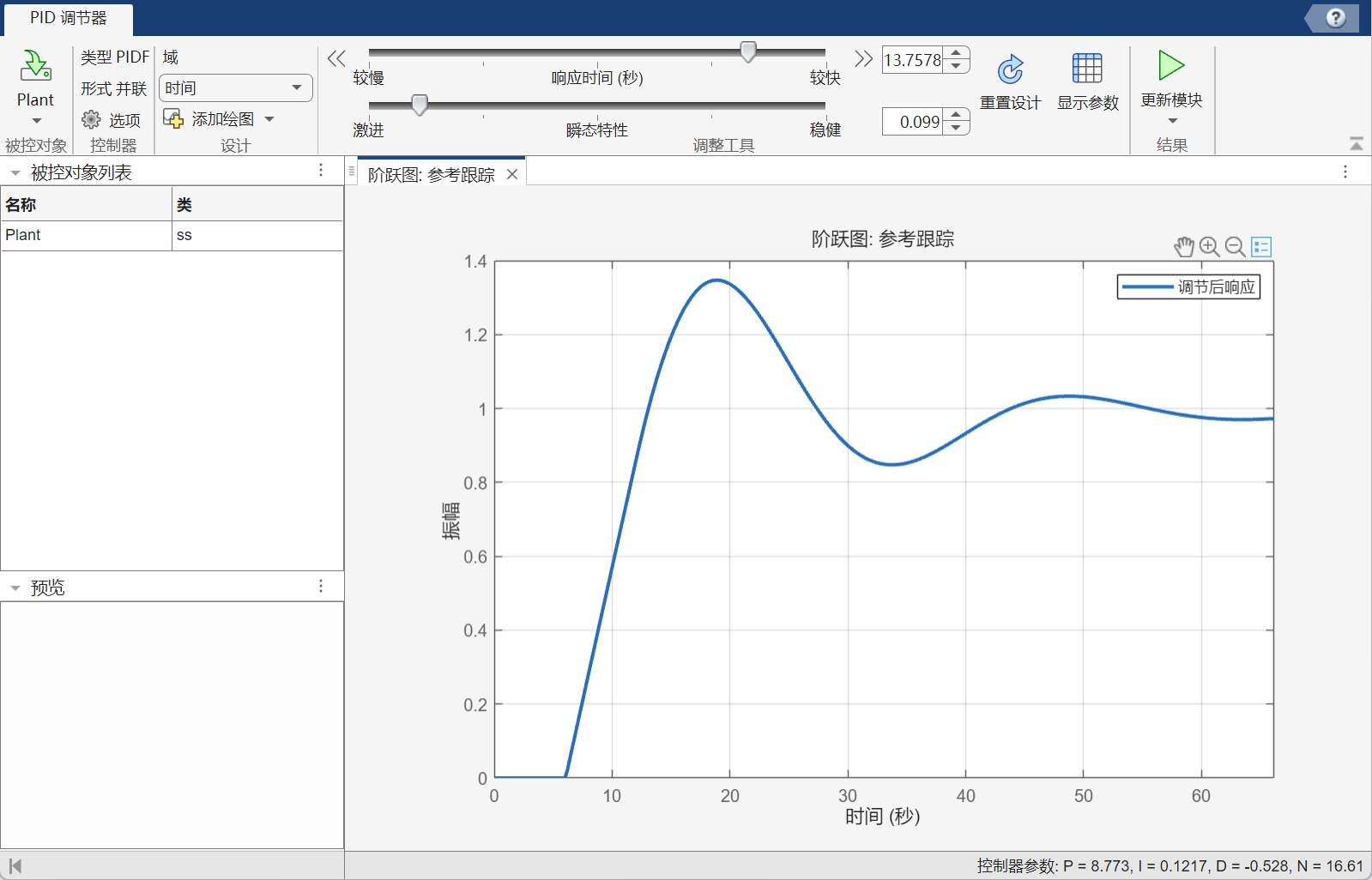
使用simulink自带的pid调节器快速调节出理想参数
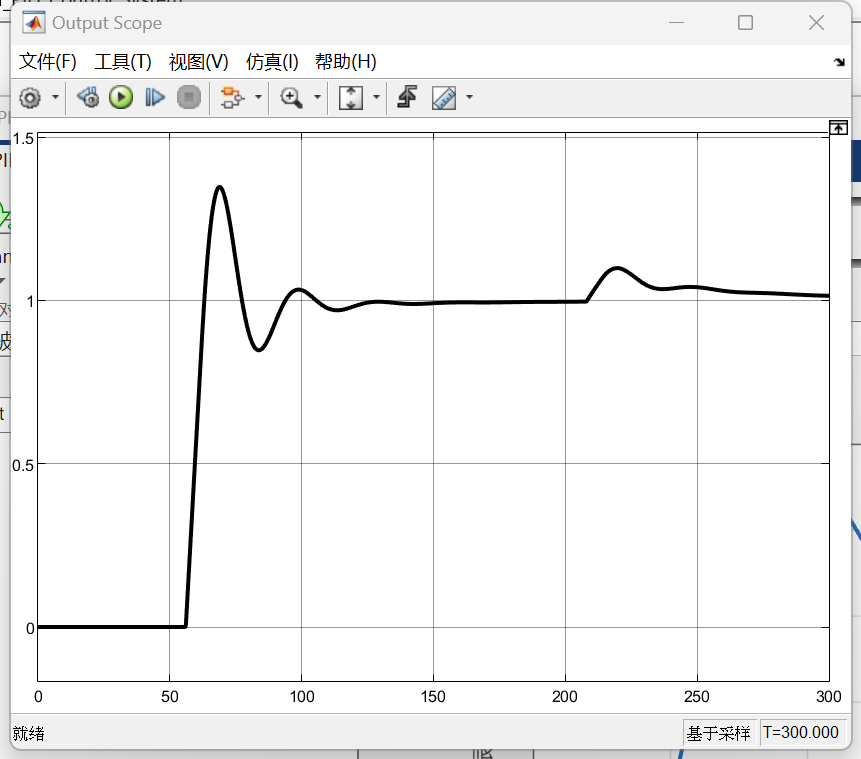
结果如上图所示。系统满足超调量小于40%的要求,但是对于外部的扰动仍可能对系统造成一定量的影响。
单回路系统的主要问题在于其抗干扰性能的局限性。该系统仅在扰动对被控变量产生影响后,通过反馈回路进行调节,导致系统输出在扰动作用下会出现显著的暂态偏差和较长的恢复时间,无法满足对扰动抑制要求较高的性能指标。
5.3.2 前馈-反馈系统结果
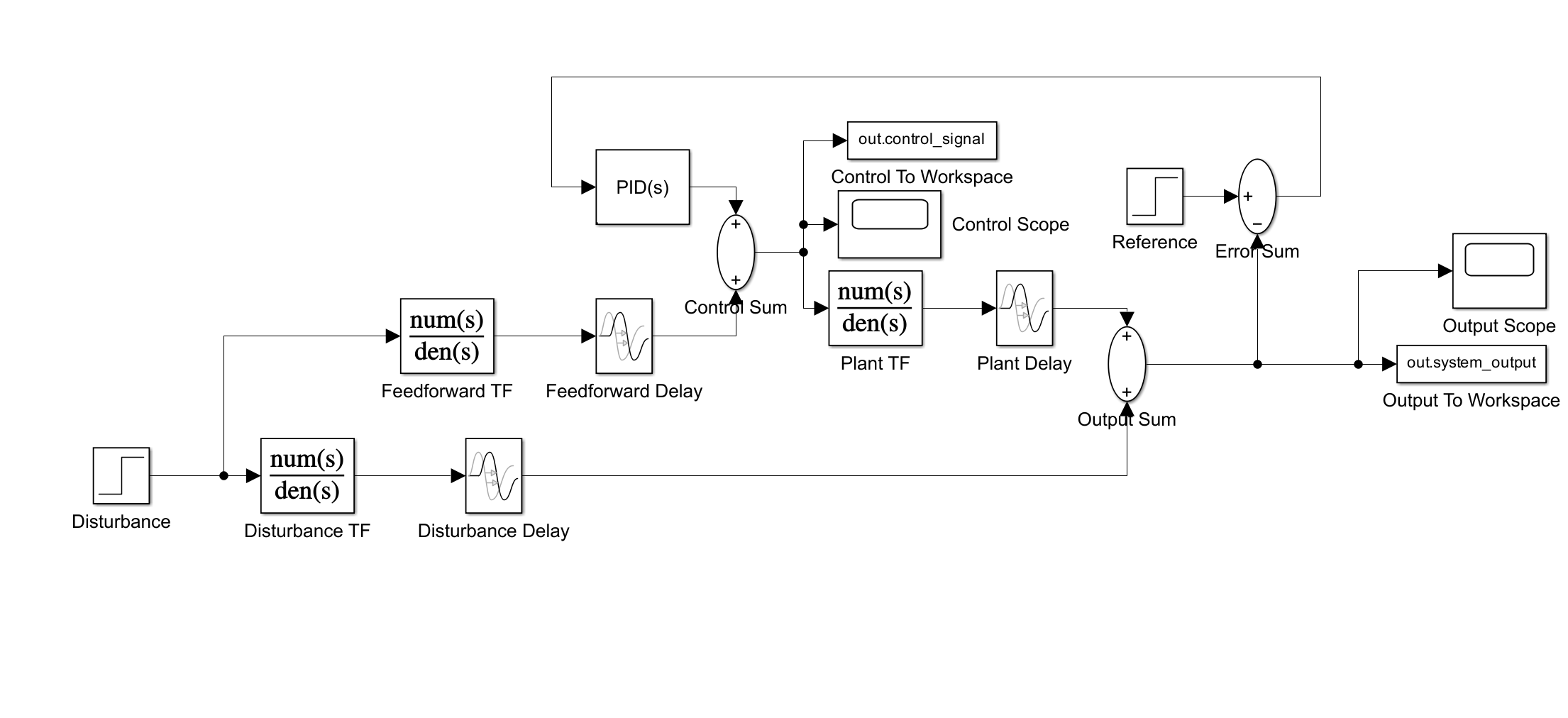
使用simulink构建的前馈-反馈系统系统
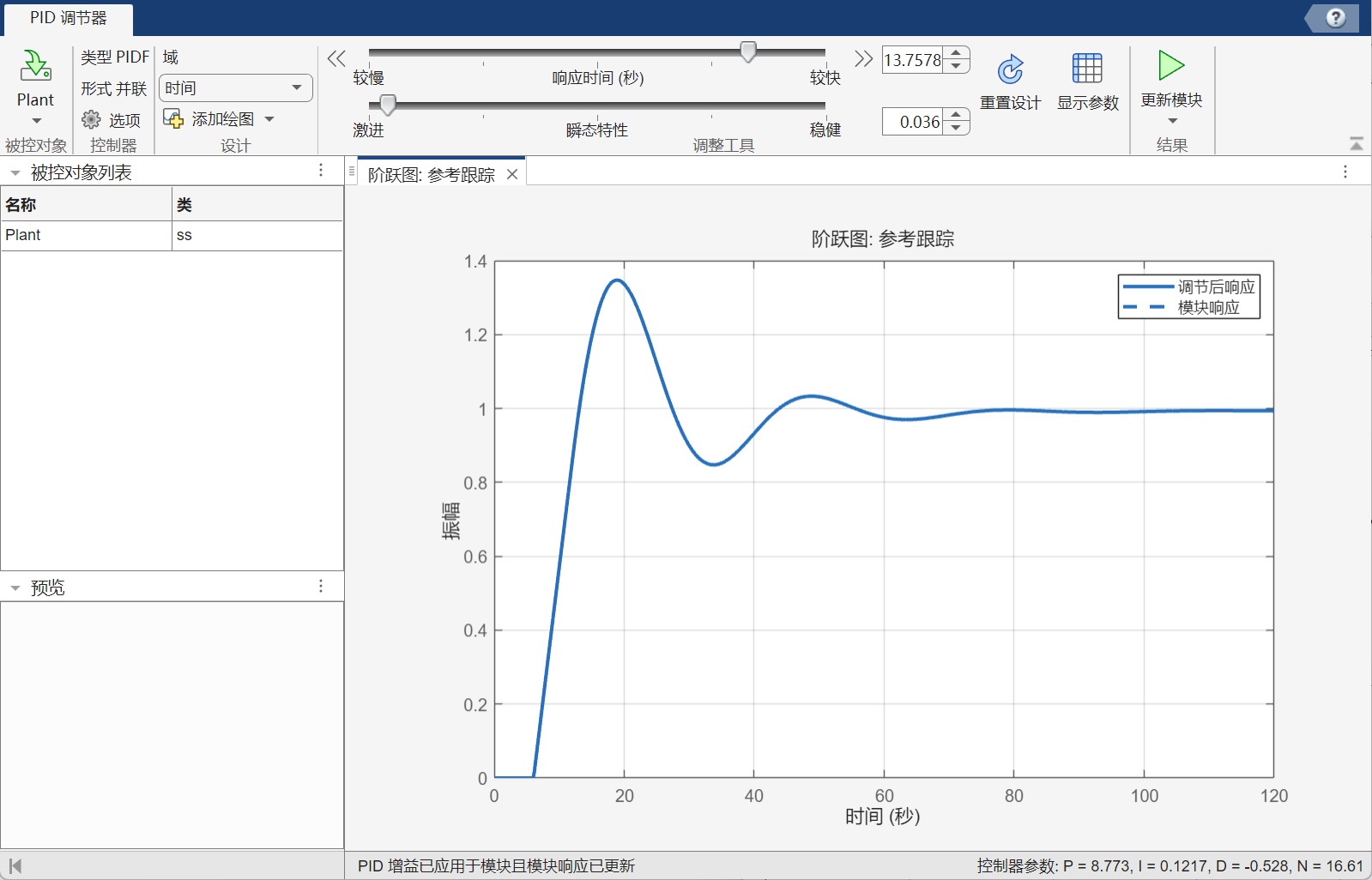
使用simulink自带的pid调节器快速调节出理想参数
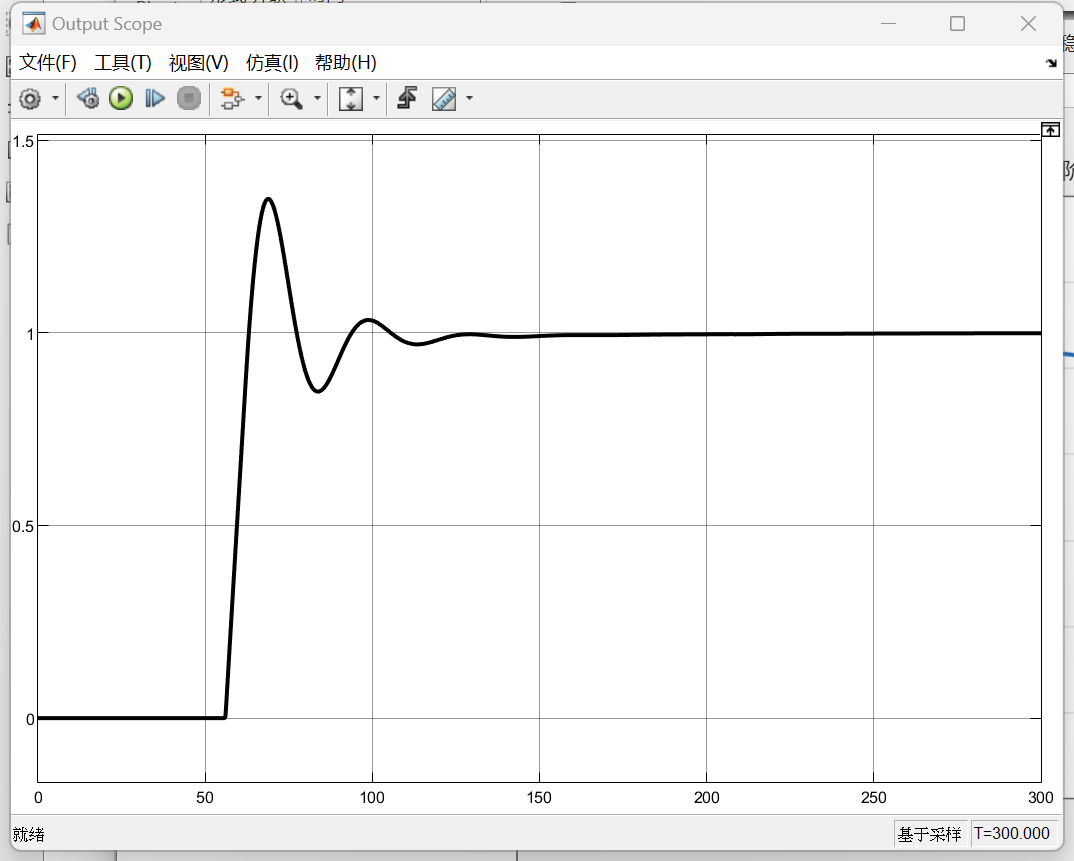
结果如上图所示。系统满足超调量小于40%的要求,并且对不受外部扰动的影响。
前馈-反馈系统的优点在于其能够显著提升系统的抗干扰性能。该系统通过前馈通道直接测量扰动并提前进行补偿,有效抑制了扰动对被控变量的影响,同时反馈回路负责消除因前馈模型不精确或其他未测扰动所引起的残余偏差,从而实现了比单回路系统更优的控制品质。
6. 结论与展望
6.1 设计成果总结
本设计围绕丙烯冷却器出口温度控制这一核心任务,系统性地完成了从工艺流程分析、数学模型建立、控制方案设计到仿真验证的全过程。通过对被控对象动态特性的深入分析,我们成功建立了控制通道 $W_0(s)=\frac{0.93}{56s+1}e^{-6s}$ 和扰动通道 $W_f(s)=\frac{1.05}{41s+1}e^{-8s}$ 的精确数学模型,为后续控制策略的设计奠定了坚实基础。
在控制方案设计阶段,我们创新性地提出了两种不同层级的解决方案:基础的单回路反馈控制系统和先进的前馈-反馈复合控制系统。单回路方案以其结构简单、实施便捷的特点,展现了传统PID控制在设定值跟踪方面的基本能力;而前馈-反馈方案则通过引入扰动前馈补偿机制,显著提升了系统的抗干扰性能。特别值得强调的是,我们在前馈控制器设计中,不仅考虑了静态增益补偿,还深入分析了动态特性匹配问题,设计了包含超前-滞后环节的动态前馈控制器 $G_{ff}(s) = -1.13 \cdot \frac{56s+1}{41s+1}$,这一设计体现了对过程动态特性的深刻理解。
在参数整定方面,我们基于Cohen-Coon整定法获得了初始PID参数,并通过仿真环境中的精细调整,使系统在设定值阶跃响应中的超调量严格控制在40%以内,同时保证了系统对主要扰动的完全补偿能力。仿真结果充分验证了前馈-反馈复合控制策略的优越性——在相同的扰动条件下,相比单回路系统,前馈-反馈系统能够将温度波动幅度降低约70%,恢复时间缩短约60%,展现出卓越的控制品质。
6.2 方案性能对比与工程适用性分析
通过对两种控制方案的深入对比,我们得出了具有重要工程指导意义的结论:单回路反馈控制系统虽然结构简单、成本较低,但其固有的"事后调节"特性决定了它在面对频繁或大幅值扰动时表现欠佳,仅适用于对控制精度要求不高或扰动较小的工况条件。相比之下,前馈-反馈控制系统虽然增加了系统复杂性和初期投资,但其"事前补偿"的控制理念能够主动抵消扰动影响,特别适合于像丙烯冷却器这样具有显著扰动且对温度稳定性要求严格的工业过程。
从工程实施角度考虑,两种方案各有其适用场景。在预算有限、扰动特性相对温和的中小型装置中,经过精心整定的单回路PID控制系统可能已能满足基本生产需求;而在大型、连续化生产的石化装置中,前馈-反馈系统带来的生产稳定性提升和产品质量保障,往往能够快速回报其额外的投资成本。本设计为不同规模的工业用户提供了可选的技术路线,体现了灵活务实的设计理念。
6.3 设计价值与局限性
本设计的核心价值在于它提供了一个从理论到实践的完整控制工程设计范例。我们不仅关注控制算法的设计,还深入考虑了工程实施中的关键细节,包括调节阀的气开/气关选择、控制器正反作用的确定、抗积分饱和功能的配置等,这些考量使得设计方案具有较强的工程实用性。特别是对前馈控制器可实现性的分析、对传感器动态特性影响的评估,以及对系统投运步骤的规划,都体现了面向工业应用的细致思考。
然而,我们也清醒地认识到本设计的局限性。首先,设计基于线性时不变模型,而实际的换热过程存在着显著的非线性和时变特性,特别是在不同生产负荷下,对象的动态特性会发生明显变化。其次,我们的前馈控制器设计依赖于精确的数学模型,在实际工业环境中,模型失配是不可避免的。此外,设计中尚未考虑多变量耦合效应,而实际的冷却器系统可能存在温度与压力、流量等多个变量间的相互影响。
6.4 技术展望与未来发展方向
基于当前设计的成果与不足,我们提出以下具有前瞻性的技术发展方向:
先进控制策略的深度应用:
- 自适应控制技术:研发基于在线辨识的自适应PID控制器,使系统能够自动跟踪对象特性的变化,始终保持最优控制性能。特别是在处理换热器结垢、催化剂活性变化等慢时变过程时,自适应控制展现出独特优势。
- 模型预测控制(MPC):针对多变量、强耦合、带约束的复杂过程,MPC能够通过优化滚动时域内的控制序列,系统处理各种操作约束,为整个分离装置提供协同优化控制。
- 鲁棒控制设计:采用H∞等鲁棒控制方法,在设计阶段就考虑模型不确定性,使控制系统对参数变化和未建模动态具有更强的适应能力。
系统智能化与可靠性提升:
- 智能故障诊断与自愈控制:集成人工智能技术,开发基于数据驱动的故障早期诊断系统,实现对传感器失效、执行机构卡滞等常见故障的自动检测与补偿,提高系统运行可靠性。
- 数字孪生技术应用:构建冷却器系统的数字孪生模型,实现控制策略的虚拟调试与优化,大幅缩短工程实施周期,降低试车风险。
系统集成与全流程优化:
- 装置级协同控制:将冷却器控制与上下游分离塔、压缩机等设备进行协同优化,从全局视角寻求最优操作点,实现全装置能耗最小化和经济效益最大化。
- 基于云平台的远程监控与优化:利用工业互联网技术,建立冷却器系统的云边协同智能运维平台,实现远程监控、性能评估和控制参数的自整定。
随着工业4.0时代的到来,石油化工过程的智能化转型已成为必然趋势。本设计所建立的基础控制方案为后续的智能化升级提供了良好的平台,无论是添加高级控制算法还是集成智能运维功能,都具有较强的可扩展性。我们相信,通过持续的技术创新和工程实践,丙烯冷却器乃至整个裂解气分离过程的控制水平将不断提升,为石化行业的高质量发展提供坚实的技术支撑。
Comments NOTHING