拖动电机

直流电机

直流电动机的基本组成

直流电机

• 定子
  • 机座
  • 主磁极
  • 主极铁芯
  • 励磁绕组
  • 换向器
  • 电刷
  • 端盖
• 转子
  • 电枢铁芯
  • 电枢绕组
  • 换向器
  • 转轴
  • 轴承
  • 风扇

感应电动势与电磁转矩

感应电动势

$E_a = C_e\Phi n$
其中，电动势常数 $C_e = \frac{pN}{60a}$
$p$ ： 磁极对数
$N$ ： 电枢绕组的总导体数
$a$ ： 并联支路对数
$\Phi$ ：每极磁通
$n$ ：转速 （r / min）

电磁转矩

$T = C_T \Phi I_a$
其中，转矩常数 $C_T = \frac{pN}{2\pi a}$

转矩常数与电动势常数的关系式
$C_T = 9.55C_e$

直流电机特性的基本关系式

	电动机	发电机
电枢回路电压	$U_a = E_a +I_aR_a$	$E_a = U_a + I_aR_a$
机电能量转换	$E_a = C_e\Phi _n$ $T = C_T\Phi I_a$	$E_a = C_e\Phi _n$ $T = C_T\Phi I_a$
机械系统转矩	$T=T_L=T_0+T_2$	$T_1=T+T_0$
励磁和主磁通	$I_f = U_f / R_f$ $\Phi = f(I_f,I_n)$	$I_f = U_f / R_f$ $\Phi = f(I_f,I_n)$
功率平衡	$P_1 = P_M + p_{Cua}$ $P_M = P_0+P_2$	$P_1 = P_M + P_0 = P_2 + \Sigma P$ $\Sigma P = p_{Cua} + P_m + p_{Fe}$

其中，

• $U_a$ ： 电枢两端的端电压
  $E_a$ ： 电枢感应电动势
  $I_a$ ： 电枢电流
  $T$ ： 电磁转矩
  $T_L$ ： 负载转矩
  $T_0$ ： 空载转矩
  $T_1$ ： 原动机拖动发电动机的拖动转矩
  $T_2$ ： 电动机的输出转矩
  $n$ ： 电动机的转速
  $U_f$ ： 励磁电压
  $I_f$ ： 励磁电流
  $\Phi$ ： 主磁通
  $\Omega$ ： 机械角速度 $\Omega = \frac{2\pi n}{60}$

对于电动机：

• $P_1$ ： 电动机从电源输入的电功率， $P = UI_a$
  $P_M$ ： 电磁功率， $P_M = T\Omega = E_a I_a$
  $p_{Cua}$ ： 电枢回路总的铜损耗
  $p_0$ ： 空载损耗，包括铁损耗$p_{Fe}$和机械摩擦损耗$p_m$， $p_m = p_0 + P_2$
  $P_2$ ：转轴上输出的机械功率，$P_2 = T_2 \Omega$

总结

• 对于电动机
  输入功率经过铜损耗（$P = I^2R$）剩下的为电磁功率
  电磁功率经过空载损耗 剩下来的是输出功率

例题

已知一台他励直流电动机的数据为$P_N = 75kW,U_N=220V,I_{aN}=383A,n_N=1500rpm,R_a=0.0192\Omega$，忽略磁路饱和的影响。
求：额定运行时的电磁转矩、输出转矩、输入功率和效率

• 求出感应电动势和电磁功率
• 有电磁转矩$T = C_T\Phi I_a$
  $I_a = \frac{P_M}{C_e\Phi n}$
  得 $T = 9.55\frac{P_M}{n}$
• 输出转矩$T = 9.55\frac{P_N}{n}$

直流电机的部分特性

串励直流电动机

对于串励直流电动机，励磁电流与电枢电流相同
有转速 $n = \frac{E_a}{C_e \Phi} = \frac{U - I_a R_a}{C_e \Phi}$
如果磁路没有饱和，速度会变快，可能飞车。
所以，串励电动机不允许在负载低于额定的 15% 下运行

他励直流电动机的机械特性

机械特性表达式：
$n = \frac{E_a}{C_e\Phi} = \frac{U - I_a R_a}{C_e\Phi} = \frac{U}{C_e \Phi} - \frac{R_a}{C_e C_T \Phi ^2} T$
改写成
$n = n_0 - \beta T = n_0 - \Delta n$
式中，
$n_0$ 为 $T = 0$时的转速，称为理想空载转速，$n_0 = \frac{U}{C_e\Phi}$
$\beta$ 为 机械特性的斜率， $\beta = \frac{R_a}{C_e C_T \Phi ^2}$
$\Delta n$ 为转速降，$\Delta n = \beta T$

可以做出一个曲线，称为固有机械特性曲线，存在以下特点：
1. 随着电磁转矩增大，转速降低
2. 硬特性

关于硬特性与软特性
机械特性的斜率越大，机械特性越软
对于他励电动机，机械特性通常偏硬

人为机械特性

他励直流电动机的电压、磁通、电枢回路电阻人为地改变后，其对应的机械特性称为人为机械特性
主要有三种：
1. 电枢回路串电阻
2. 改变电枢电压
3. 减弱磁通

例题

一台他励直流电动机的额定功率 $P_N = 75\mathrm{kW}$ ，额定电压 $ U_N = 220\mathrm{V}$ ，额定电流 $I_N = 385\mathrm{A}$ ，额定转速 $n_N = 1000\mathrm{r/min}$ ，电枢回路总电阻 $R_a = 0.01824\Omega$ ，电动机带额定恒转矩负载运行。若要求转速调到 $400\mathrm{r/min}$ ，假定 $T_0$ 不变。求：
（1）采用电枢串电阻调速时，电枢回路需串入多大的电阻？该转速下电动机的效率是多少？
（2）采用改变电枢电源电压调速时，电源电压应调到多少伏？电动机的效率是多少？

对于问题一
1. 先求出要求转速下的感应电动势
公式$E = C_e\Phi n$，需要知道$C_e\Phi$
通过已知条件求出来
$U_N - I_NR = C_e\Phi n_N$
得$C_e\Phi = 0.213$
求得 400rpm下感应电动势为 85.2V
2. 串入电阻加上原来的电阻应该分走$(220 - 85.2)V$，容易计算
3. 输出功率还有一个空载损耗，算出空载损耗
额定转速下 电磁功率减去输出功率就是空载损耗
空载损耗满足 $p = T\Omega$
所以可以算出400rpm下空载损耗
然后计算效率

对于问题二
1. 算出理想空载转速
$n = \frac{U_N}{C_e\Phi}$
得出$\Delta n$
2. 得出空载电压
3. 得出输入功率和输出功率
4. 计算效率

他励直流电动机的制动

• 能耗制动
  电源断开，串入电阻
• 反接制动
  电源反向，串入限流电阻
• 倒拉反转制动
  电源正向，串入电阻
  负载拖动电机旋转，使得电机超过空转转速。电机提供制动力
  动能 >> 热能
• 回馈制动
  动能 >> 电能

例题

他励直流电动机的额定功率$P_N = 75kW$，额定电压$U_N = 220V$，额定转速$n_N = 1000r/min$，额定电流$I_n=385A$, 电枢回路总电阻$R_a = 0.018242\Omega$，电动机拖动位能性负载$T_L=0.8T_N$运行。若要求电机一转速$250rpm$下放负载，求：
采用能耗制动运行时，电枢回路应该串入多大的电阻？该电阻上损耗的功率有多大？
采用倒拉反转运行时，电枢回路应该串入多大的电阻？该电阻上损耗的功率是多少？
采用改变电枢电源电压的反向回馈制动运行时，电枢回路不串电阻，反向电枢电源电压应该调到多少$V$?若反向电枢电源电压调到额定电压，下放速度变为多少？

• 对于题一和题二，关键地方在于求出感应电动势和回路电流。
  通过题给条件求得$C_e\Phi$
  容易求得$E_a = C_e\Phi n$
  因为$T_L = 0.8T_N$，容易求得电流
• 对于题三，需要求出给定转速下损耗部分的转速
  理想状态的空转转速为$n = \frac{U}{C_e\Phi}$
  现实情况的转速为$n=\frac{U - IR}{C_e\Phi}$
  进而求得给定转速下生成的电压，或者给定电压下的转速

章节问答题

换向器在直流发电机和直流电动机中起什么作用

整流（发电机）
逆变（电动机）

为什么直流电机的转子铁芯要用表面有绝缘层的硅钢片叠压而成

减少涡流损耗
硅钢片本身电阻率较高，叠加并绝缘更加减少涡流通路，减少铁损发热

主磁极和电枢铁芯都是电机磁路的组成部分，但其冲片材料为什么一个用薄钢板，一个用硅钢片

主磁极铁芯通过的是恒定方向的主磁通，不产生涡流损耗，可以降低成本
电枢铁芯旋转时，其内部磁场交变，会产生巨大的涡流损耗，必须使用硅钢片叠压减少涡流损耗

什么是直流电机的电枢反应?其结果是什么?

定义：电枢磁场对主磁场的影响和作用
结果：

• 磁场畸变（物理中性线偏移）： 使气隙磁场发生扭曲，原来的几何中性线不再是的磁感应强度为零的位置，物理中性线逆转向（发电机）或顺转向（电动机）偏移。这会给换向带来困难，易产生火花。
• 去磁效应： 电枢磁动势的交轴分量使主磁场一半增强、一半削弱，但由于磁路饱和，增强的部分少于削弱的部分，导致每极下的合成磁通量略有减少。

简述直流电动机的工作原理。

基于“载流导体在磁场中受力”的电磁力定律。

1. 将直流电源接在两电刷之间，电流由正刷流入，经电枢绕组后从负刷流出。

2. 在N极下的导体电流方向为一个方向，在S极下的导体电流方向为另一个方向。

3. 所有导体均受到方向相同的电磁力，形成驱动转子旋转的电磁转矩。

4. 换向器的作用是确保导体从一个磁极下转到另一个磁极下时，其电流方向能及时改变，从而保证电磁转矩的方向始终一致，电机持续旋转。

主磁通既连着电枢绕组又连着励磁绕组，为什么只在电枢绕组里产生感应电动势?

励磁绕组静止，并且主磁通恒定
不具备产生电动势的必要条件

一台他励直流电动机，如果励磁电流和被拖动的负载转矩不变，而仅仅提高电枢端电压，试问电枢电流、转速变化如何?

负载转矩不变 >> 电磁转矩不变
电磁转矩不变 >> $T$ 不变 >> $T = C_T\Phi I$ >> 电枢电流不变
提高电枢电压 >> $U - IR = C_e\Phi n$ >> 转速上升

如何判别直流电机运行于发电机状态还是电动机状态?它们的$T,n,E_a,U_a,I_a$的方向有何不同?能量转换关系如何?

物理量	电动机状态	发电机状态
电动势$E_a$	$E_a<U_a$	$E_a >U_a$
电枢电流$I_a$	与电源电压$U_a$同向	与电源电压$U_a$反向
电磁转矩$T$	与转速同向	与转速反向
能量转换	电能 >> 机械能	机械能 >> 电能

为什么直流电动机直接起动时起动电流很大?

启动时候转速为0
根据公式 $U = E_a + I_aR_a$，启动电流$I = U / R$
因为电枢电阻很小，所以启动电流相当大

他励直流电动机起动过程中有哪些要求?如何实现?

要求：

• 起动转矩足够大，以克服静摩擦。

• 起动电流不能过大，以免烧坏电枢绕组和冲击电网。

实现方法：电枢回路串电阻起动 或 降压起动。核心都是在起动时降低电枢绕组上的实际电压，从而限制起动电流。

他励直流电动机起动时，为什么一定要先把励磁电流加上?若忘了先合励磁绕组的电源开关就把电枢电源接通，这时会产生什么现象(试从T=0和T=T两种情况加以分析)?当电动机运行在额定转速下，若突然将励磁组断开，此时又将出现什么情况?

为什么先加励磁电流？
没有励磁电机无法启动，会烧坏电枢

运行时励磁断开？
根据公式$n = \frac{E}{C_e\Phi}$
如果负载较重，转速可能下降，导致电流加大，烧毁电枢
如果转速不变，导致感应电动势下降，电流加大，烧毁电枢
如果负载较轻，转速上升，导致飞车

直流串励电动机能否空载运行?为什么?

不能。会飞车（参见上一题）

直流电动机用电枢回路串电阻的方法起动时，为什么要逐级切除起动电阻?若起动电阻留在电枢电路中，对电动机运行有什么影响?若切除太快、会带来什么后果?

逐级移除电阻：随着转速上升，反电动势增大，电流减小。为了维持输出转矩，需要保持电流。
电阻留在电路中？转速上升，电流下降，输出转矩下降，导致动力不足。并且电阻耗电，降低效率
切除太快？电枢电流过大，冲击电网和电机

他励直流电动机有哪些方法进行调速?其特点是什么?

调速方法	调节电枢电压	电枢串电阻	减弱磁通
实现	改变电源电压U	在电枢回路串电阻R	增大励磁回路电阻，减小励磁电流If
调速方向	低于额定转速（向下调）	低于额定转速（向下调）	高于额定转速（向上调）
特性	无级调速，硬度不变，效率高	有级调速，特性变软，效率低	无级调速，硬度不变，调速范围有限

直流电动机的电动与制动两种运行状态的根本区别是什么?

根本区别在于电磁转矩$T$与转速$n$的方向关系
电动状态： $T$与$n$的方向相同，电磁转矩是驱动转矩
制动状态： 方向相反，是制动转矩，电机吸收机械能

实现倒拉反转反接制动和回馈制动的条件各是什么?

倒拉反转制动：

1. 电机接正向电源。

2. 电枢回路串入大电阻。

3. 被位能性负载拖着反转（n为负）或正向超速（n > n0），稳定运行于第IV象限。

回馈制动：

1. 电机端电压保持接通。

2. 电枢回路无大电阻（工作在固有特性附近）。

3. 在外部动力（如下坡、降压调速）驱动下，电机的实际转速 n 高于其理想空载转速 n0（n > n0）。

三相异步电动机

三相异步电动机的数学描述

转差率

• 称同步转速$n_0$与转子转速$n$之差为转差
  转差与同步转速之比为转差率，用$s$表示
  $$s = \frac{n_0 - n}{n_0} * 100\%$$
  一般情况下，空载转差率小于 0.5% ,满载转差率小于 5%

同步转速

$$n_0 = \frac{60f_1}{p}$$
其中，

• $f_1$ 为交流电流频率
  $p$ 为极对数

转差频率

$$f_2 = sf_1$$
其中，

• $f_2$ 为转差频率

一台$50Hz$的三相异步电动机，$n_N = 730rpm$，空载转差率为$s_0 = 0.267\%$。
求： 极对数、同步转速、实际空载转速、额定负载时的转差率和转差频率

1. 极对数：
   $n = 60f_1/p$，最接近730rpm的是 p = 4
2. 同步转速： 易得750rpm
3. 实际空载转速：
   $n^\prime _0 = n_0 (1 - s_0) = 748rpm$
4. 额定负载转差率/转差频率：
   $s_N = (n_0 - n_N)/n_0 = 2.67\%$
   $f_2 = s_Nf_1 = 1.335Hz$

T型等值电路

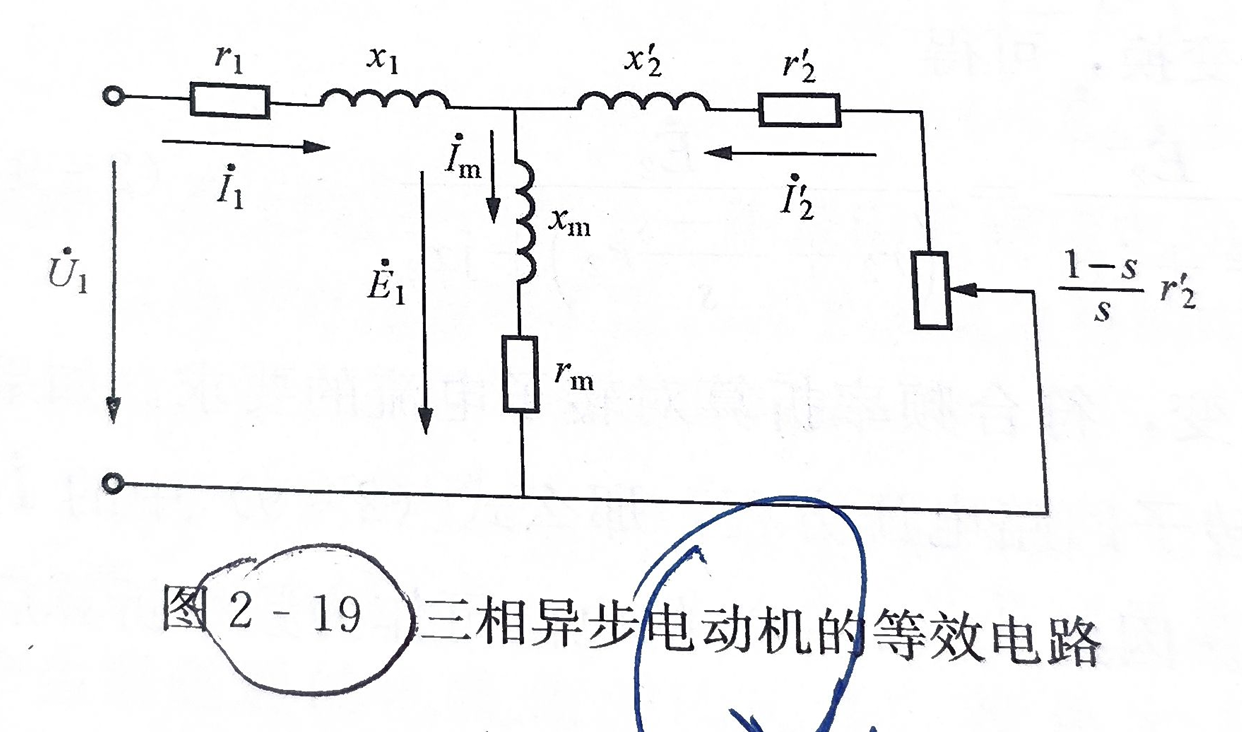
其中，
- $r_1,x_1$为定子绕组的电阻和漏电抗
- $r_2,x_2$为转子绕组的电阻和漏电抗
- $r_m,x_m$为励磁绕组的电阻和漏电抗

三相异步电动机的机械特性

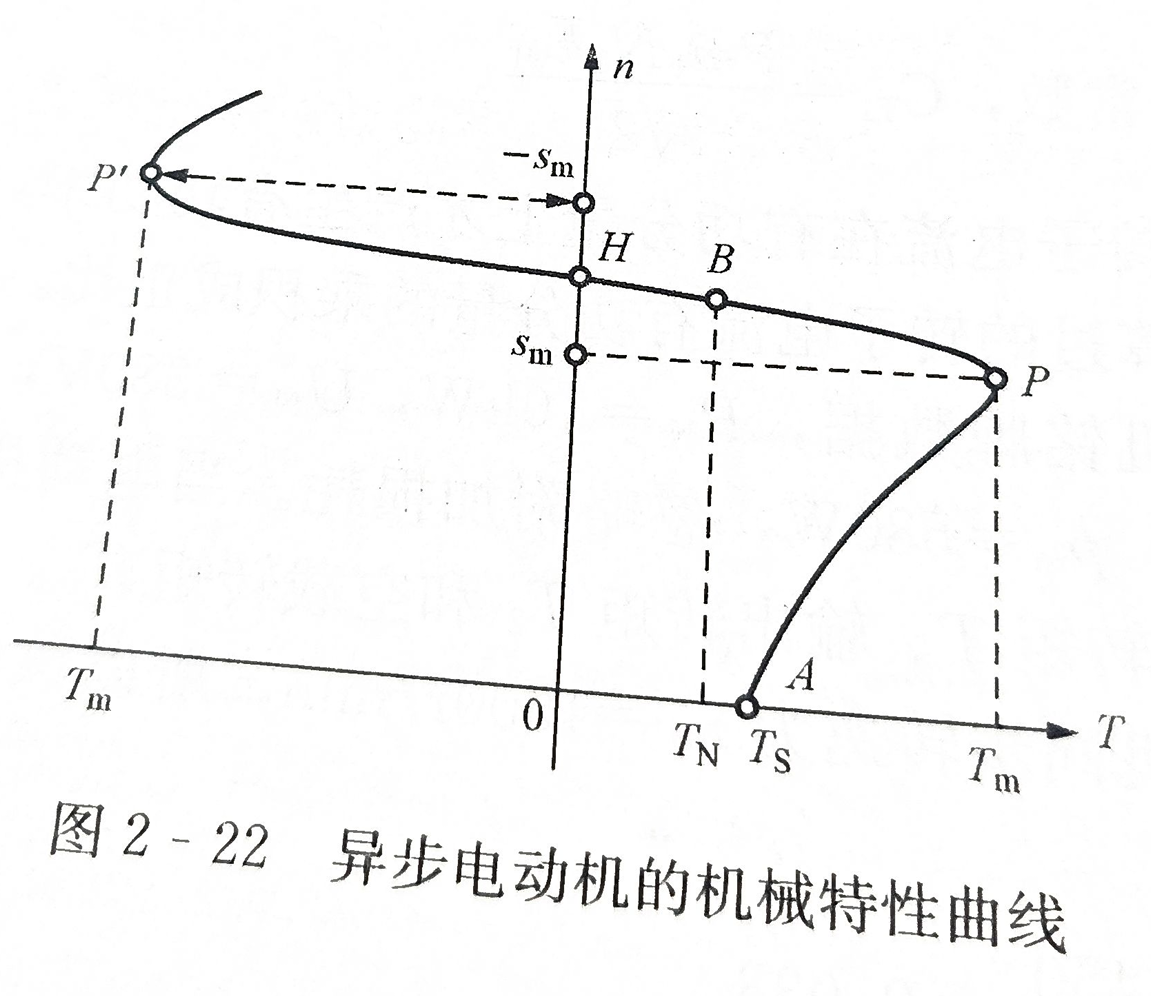
如图所示：

• $s_m$ 为最大转差率

存在

点位	转矩	转速	转差率
空载H	0	$n_0$	0
额定B	$T_N$	$n_N$	$s_n = \frac{n_0 - n_N}{n_0}$
临界点P	$T_M = k_mT_N$		$s_m = s_n(k_m\pm (\sqrt{k_m^2 - 1}))$
起动点A	$T_S = \frac{2T_M}{\frac{1}{s_m}+\frac{s_m}{1} }$	0	1
一般点	$T = \frac{2T_M}{\frac{s}{s_m}+\frac{s_m}{s} }$

电机过载倍数：$k_m = \frac{T_M}{T_N}$

人为机械特性

人为改变电动机的机械参数可以得到不同的机械特性
对于改变电阻的行为,可以得到不同的转差之比

$$\frac{s_1}{s_2} = \frac{s_m}{s_m^\prime} = \frac{R_2^\prime}{R_2^\prime + R_\Omega ^\prime}$$

做题

某绕线转子异步电动机参数如下：
$P_N = 75kW,I_{1N}=144A ，U_{1N}=380V,E_{2N}=399V,I_{2N}=166A,n_N=1460rpm,k_m = 2.8$

问题1：负载转矩为$T_z=0.8T_N$，要求转速$n_B=500rpm$时，转子每相串入多少电阻？

对于串入的电阻，有公式
$$\frac{s_1}{s_2} = \frac{s_m}{s_m^\prime} = \frac{R_2^\prime}{R_2^\prime + R_\Omega ^\prime}$$
现在缺少两个转差率以及转子电阻
有公式
$$s_m = s_n(k_m\pm (\sqrt{k_m^2 - 1}))$$
$$s_m^\prime = s_n^\prime(\frac{T_M}{T}\pm (\sqrt{\frac{T_M}{T}^2 - 1}))$$
$$R_2^\prime = \frac{S_NE_{2N}}{\sqrt{3}I_{2N}}$$